Beyond "Bitter Twitter": Crowd-Photography for the Cyber-Tahrir Square
BY MICAH L. SIFRY | Tuesday, July 10 2012 - TechPresident
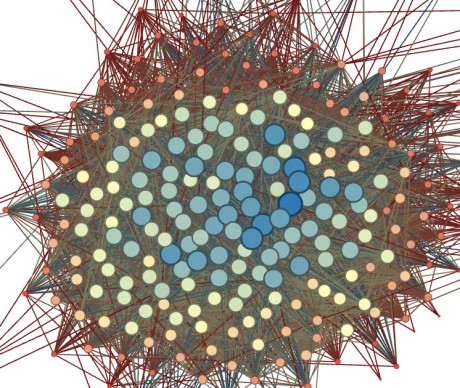
A close-up view of @davidaxelrod's Twitter footprint from July 6, 2012
"This election may be remembered as the Bitter Twitter campaign," former Bush adviser Mark McKinnon said recently. With both campaigns avoiding offering any big new ideas, he predicted that "we are likely to see the next [few] months as a furious and relentless exchange of messages that aren't much longer or deeper than 140 characters."
Is that all that can be said about the daily Twitter wars between the Romney and Obama camps? To get a bigger picture — or rather, as you will see below, to get several bigger pictures — I turned to Marc A. Smith, chief social scientist with the Connected Action consulting group, who has long studied computer-mediated collective interaction. For the last few years, he and his colleagues have been doing what he chirpily calls "crowd photography for the cyber-Tahrir Square," using a sophisticated network mapping tool called NodeXL they've developed as a free extension to Excel. And the graphs they make offer a whole new way of seeing the connections among people, events and ideas as they coalesce online. Here, for example, is the conversation online when the "pink slime" controversy was at its height. Here's a chatter map for the controversy over "Fast and Furious"when Attorney General Eric Holder and Rep. Darrell Issa recently locked horns.
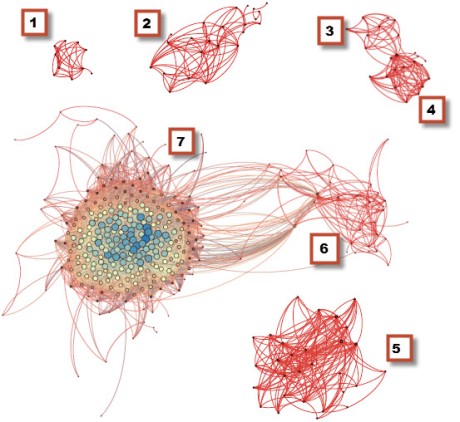
But how to read them? Take this snapshot of the public conversation on Twitter after the first day of this year's Personal Democracy Forum conference. Here, Smith got data on 711 Twitter users whose recent tweets contained the hashtag "#pdf12." Users are clustered together if they have lots of connection to each other, based on who follows whom, who replies to whom, and who mentions whom, and then each cluster is given its own rectangle based on those users having used similar hashtags in addition to #pdf12, with those listed in order of prominence.
Blue lines are links NodeXL builds when one user mentions, replies to or retweets another. Green lines represent people who follow each other. The "isolates" — in this case in the bottom right — are users who don't connect to others on the graph. "Reading" the graph (which I did with Smith's help), you can learn several things about the social landscape of the #PDF12 community.

There are three major subgroups that were tweeting from and about PDF12. First and largest, in the top left corner, are the open-government folks, whose top three hashtags after #PDF12 were #opengov, #opendata and #OGP (for the Open Government Partnership). At the center of this cluster, not surprising, you can see the Twitter avatars of power-tweeters like O'Reilly Media's Alex Howard (@digiphile), who covers open government and open data on a daily, even hourly, basis.
The second group in the top left are the PDF progressives, netroots folks who had likely just attended the annual Netroots Nation conference in Providence, RI. Their usage of hashtags like #NN12 and #ows (Occupy Wall Street) is a sure giveaway of their closeness to each other.
And third, in the bottom left corner of the graph, are the PDF netheads (you can recognize Zeynep Tufekci @techsoc, for example) who were paying closest attention to issues like online privacy, SOPA and PIPA.
A few additional observations are in order. First, there's not a lot of hierarchy to this community of individuals. There are lots of bilateral connections between people, as evinced by all the crosshatching green and blue lines. Second, the relatively large number of "isolates" in the bottom right corner is a good sign, Smith told me. It suggests that #PDF12 was also reaching beyond its core audience, and shows that we're not a completely "built-out" network. In other words, that there's room for growth. Network maps for other conferences, he says, often show that they're just speaking to themselves. And finally, the small cluster at the bottom of the middle of the graph indicates that there were probably some people using "pdf12" in their tweets during the conference who had absolutely nothing to do with the event, but maybe had some other common point of contact, such as linking to this document: http://www.eluniversal.com.mx/graficos/pdf12/recuento-eleccion.pdf.
Axelrod vs Fehrnstrom
Now take a look at how the Twitter conversation coalesces around two leading online surrogates for the Obama and Romney campaigns, David Axelrod and Eric Fehrnstrom. Axelrod is the Obama campaign's senior strategist; Fehrnstrom is one of Romney's senior campaign advisors. I asked Smith to run NodeXL against a recent list of Twitter users who either mentioned @davidaxelrod or @ericfehrn, and this is what he found.
Now take a look at how the Twitter conversation coalesces around two leading online surrogates for the Obama and Romney campaigns, David Axelrod and Eric Fehrnstrom. Axelrod is the Obama campaign's senior strategist; Fehrnstrom is one of Romney's senior campaign advisors. I asked Smith to run NodeXL against a recent list of Twitter users who either mentioned @davidaxelrod or @ericfehrn, and this is what he found.
Obviously, Axelrod's network is different than Fehrnstrom's. He has more than 103,000 followers on Twitter, compared to Fehrnstrom's 13,000. And he tweets more often, roughly 5-6 times a day, while Fehrnstrom tweets at most two or three times. As a result, their NodeXL graphs cover very different time periods. For Axelrod, it just took 13 hours on July 6th to accumulate 790 users who mentioned "davidaxelrod" in a tweet. It took 10 days, from June 27 thru July 6, to accumulate a similar number (876, actually) of users who mentioned "ericfehrn."
Here's the snapshot of Axelrod's Twittersphere around July 6th. You can view a high-definition "zoomable" version of the graph here.

What's immediately apparent from the network of Axelrod mentioners is a) how polarized it is, and b) how much the pro-Obama side looks like a broadcast network, while the anti-Obama side looks like a dense community. The polarization isn't surprising; Smith says this pattern repeats across many NodeXL scans on topics touching on American politics. The most active people in online politics are from the passionate poles of our two-party system; this is not news, but there are some hints in these particular graphs that the online right is different than the online left, at least on Twitter. More on that in the moment.
First, the pro-Obama side, which is distinguished by people using Obama-friendly hashtags like "yeswewill" and "bettingonAmerica" as well as anti-Romney terms like "bainmitt" and "whatsmitthiding." If you zoom in closely on the people near Axelrod who are interrelated (the green clump in the upper right quadrant around him), you'll find other media players like Ben Smith (@buzzfeedben), Michael Scherer of Time (@michaelscherer) and Ben LaBolt, an Obama spokesman (@benlabolt). But the rest of the network of mentioners around Axelrod aren't part of the media insider circle--there are just lots of Twitter users who follow the Obama campaign's senior adviser who talk him up.
There's a lot of blue lines in this graph — remember, those are links NodeXL builds when one user mentions, replies to, or retweets another. Green lines represent people who follow each other. Given how well known Axelrod is on Twitter, it's not surprising to find so many people who mention him but don't follow each other — hence the prominence of the blue over the green. This is another indication that his reach online is more like a broadcast network or a brand than an interlaced community.
"There is an 'audience' cluster and two 'community' clusters," Smith explains. "Most blue lines (replies, mentions, retweets) point in to the 'community' clusters in which there is significant amounts of mutual connection. The community clusters are dense, while the broadcast or audience cluster is sparse with little interconnection. Axelrod has a powerful broadcast ability and his messages reverberate within the community clusters."
On the top right we have people who are good bets to be anti-Obama, given their prominent use of the "top conservatives on Twitter" hashtag #tcot, as well as anti-Obama terms like "fastandfurious" — a reference to the Justice Department scandal — and "obamatax." This group has no obvious hub, but it's also densely inter-connected. This is typical of conservatives who are heavy Twitter users; a lot of people joined the service starting in early 2007 who were looking for new leadership on the right, and along the way they all found each other.
Now let's look at Eric Fehrnstrom's Twittersphere. A zoomable version is here.

As noted above, comparing Fehrnstrom's online footprint to Axelrod's isn't apples-to-apples. He's not as well-known, he's not on TV as often, and he isn't as big a Twitter user. Unfortunately for the purposes of this article, there isn't an exact parallel to Axelrod in the Romneyverse, at least when it comes to their online activities. So, caveat emptor, this isn't meant to suggest that what one man is doing online is somehow "better" than the other. They're each interesting but for somewhat different reasons.
Again, the most obvious finding from looking at people mentioning "ericfehrn" on Twitter is that they're a polarized group. The ones on the left hand side of the graphic are mostly pro-Romney; the ones on the right are mostly pro-Obama. We know this from the hashtags they're using in common: "obamacare," "obamatax" "fullrepeal" and "teaparty" for the Romneyites; and "p2" "aca" and "whatisromneyhiding" for the Obamanauts. (Smith has noticed that few Republicans ever say "Affordable Care Act," by the way.) On the Obama side of the split, you can zoom in and find individuals like Donna Brazile and Paul Begala, well-known Democratic partisans; on the other side you can find GOP stalwarts like Matt Lewis and Justin Hart.
Interestingly, you can see some signs of Fehrnstrom having a small "broadcast" footprint in the arc-like groups of Twitter users on the outer edge of the left-hand cluster. These are people like the much bigger circle around Axelrod, who mention or retweet things that "@ericfehrn" says, but who aren't really connected in a more intensive way as a community of people who know each other.
Don't Think of an Echo Chamber
When I first reached out to Smith, I thought that mapping the Twitter relationships of political power players like Axelrod and Fehrnstrom might demonstrate just how much Twitter was intensifying the insider culture of Washington and elite politics, to the chagrin of people like Mark McKinnon. But after looking at these graphs, I'm not so sure that that is the only thing going on with Twitter and the presidential campaigns.
When I first reached out to Smith, I thought that mapping the Twitter relationships of political power players like Axelrod and Fehrnstrom might demonstrate just how much Twitter was intensifying the insider culture of Washington and elite politics, to the chagrin of people like Mark McKinnon. But after looking at these graphs, I'm not so sure that that is the only thing going on with Twitter and the presidential campaigns.
Yes, there are a lot of A-list types showing up on these two graphs, the sort of people who have given the Washington-centric White House Correspondents Dinner its current reputation as the "nerdprom" for the media-politics elite, plus some hardworking journalists who are just doing their jobs. But at the same time, there's a much bigger network of influential voices in the political Twittersphere around the Romney and Obama camps, as is reflected by centrality in the graphs of people like @ttjemery ("Christian and conservative" with 29,000 followers), @daggy1 (a self-described "enemy of socialism" with 27,000 followers), or @gaypatriot ("America's leading gay conservative voice"). And this active and highly networked set of people clearly leans right; none of the top independent progressives on Twitter happen to show up as significant participants in these two snapshots.
What that suggests is that after you get past the daily "Bitter Twitter" back-and-forth games that these campaigns surrogates are playing with each other and the Beltway media, there's a large secondary group of political activists, most of them conservatives, who are also engaged in chewing on the daily give-and-take of the presidential campaign. A lot of these people know and relate to each other via Twitter. If progressive activists were as engaged on Twitter, then presumably we'd see the same kind of dense green cloud in interconnections around Axelrod on the pro-Obama side of his graph as we do for Fehrnstrom on the pro-Romney side of his. Arguably, the fact that Axelrod is much more of a "celebrity" online may explain some of this difference too.
NodeXL is a powerful tool for exploring the social landscapes of public conversations about all kinds of topics, but it takes time and effort to develop the visual literacy needed to make sense of these graphs. Or, as Smith puts it, "it takes time to go from seeing something that looks like bug splatter on my windshield to 'oh, that looks interesting.'" Over the coming months, we're going to keep exploring this terrain with Smith's help, as he has kindly offered to run some queries on techPresident's behalf. (He also does customized research for a modest fee.) What would you like to explore? We can visualize the network around a person or group of people, a term or hashtag, even a url. The zeitgeist awaits.