Una medida centralidad de nodo clave en las redes es proximidad central (Freeman, 1978;. Opsahl et al, 2010; Wasserman y Faust, 1994). Se define como la inversa de la lejanía, que a su vez, es la suma de las distancias a todos los demás nodos. Como la distancia entre los nodos en los componentes desconectados de una red es infinito, esta medida no se puede aplicar a redes con componentes desconectados (Opsahl et al, 2010;. Wasserman y Faust, 1994). Este anuncio pone de relieve una posible solución temporal, lo que permite que la medida se aplique a estas redes y al mismo tiempo mantener la idea original detrás de la medida.

Esta red da un ejemplo concreto de la medida de la cercanía. La distancia entre el nodo G y el nodo H es infinita dado que no existe un camino directo o indirecto entre ellos (es decir, que pertenecen componentes separados). Mientras al menos un nodo es inalcanzable por los otros, la suma de las distancias a todos los otros nodos es infinito. Como consecuencia, los investigadores han limitado la cercanía a medida el componente más grande de nodos (es decir, medido intra-componente). La matriz de distancia para los nodos de la red de la muestra es:
| Nodos | Todos incluidos | Intra-componente | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | Lejanía | Cercanía | Lejanía | Cercanía | ||
| A | … | 1 | 1 | 2 | 2 | 3 | 3 | Inf | Inf | Inf | Inf | Inf | 0 | 12 | 0.08 | |
| B | 1 | … | 1 | 2 | 1 | 2 | 3 | Inf | Inf | Inf | Inf | Inf | 0 | 10 | 0.10 | |
| C | 1 | 1 | … | 1 | 2 | 2 | 2 | Inf | Inf | Inf | Inf | Inf | 0 | 9 | 0.11 | |
| D | 2 | 2 | 1 | … | 2 | 1 | 1 | Inf | Inf | Inf | Inf | Inf | 0 | 9 | 0.11 | |
| E | 2 | 1 | 2 | 2 | … | 1 | 3 | Inf | Inf | Inf | Inf | Inf | 0 | 11 | 0.09 | |
| F | 3 | 2 | 2 | 1 | 1 | … | 2 | Inf | Inf | Inf | Inf | Inf | 0 | 11 | 0.09 | |
| G | 3 | 3 | 2 | 1 | 3 | 2 | … | Inf | Inf | Inf | Inf | Inf | 0 | 14 | 0.07 | |
| H | Inf | Inf | Inf | Inf | Inf | Inf | Inf | … | 1 | 2 | Inf | Inf | 0 | 3 | 0.33 | |
| I | Inf | Inf | Inf | Inf | Inf | Inf | Inf | 1 | … | 1 | Inf | Inf | 0 | 2 | 0.50 | |
| J | Inf | Inf | Inf | Inf | Inf | Inf | Inf | 2 | 1 | … | Inf | Inf | 0 | 3 | 0.33 | |
| K | Inf | Inf | Inf | Inf | Inf | Inf | Inf | Inf | Inf | Inf | … | Inf | 0 | 0 | Inf | |
Para desarrollar esta medida, me fui de nuevo a la ecuación original:
donde  es el nodo focal,
es el nodo focal, 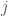 es otro nodo en la red, y
es otro nodo en la red, y 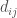 es la distancia mas corta entre estos dos nodos. En esta ecuación, las distancias están invertidas después de que se han sumado, y cuando la suma de un número infinito, el resultado es infinito. Para superar este problema durante su estancia en consonancia con la medida existente de cercanía, me aproveché del hecho de que el límite de un número dividido por infinito es cero. A pesar de que el infinito no es un número exacto, el inverso de un número muy alto es muy cercano a 0. De hecho, se devuelve 0 si introduce 1 / Inf en el programa estadístico R. Al tomar ventaja de esta característica, es posible reescribir la ecuación cercanía como la suma de las distancias La Inversa a todos los demás nodos en lugar de la inversa de la suma de las distancias a todos los demás nodos. La ecuación sería entonces:
es la distancia mas corta entre estos dos nodos. En esta ecuación, las distancias están invertidas después de que se han sumado, y cuando la suma de un número infinito, el resultado es infinito. Para superar este problema durante su estancia en consonancia con la medida existente de cercanía, me aproveché del hecho de que el límite de un número dividido por infinito es cero. A pesar de que el infinito no es un número exacto, el inverso de un número muy alto es muy cercano a 0. De hecho, se devuelve 0 si introduce 1 / Inf en el programa estadístico R. Al tomar ventaja de esta característica, es posible reescribir la ecuación cercanía como la suma de las distancias La Inversa a todos los demás nodos en lugar de la inversa de la suma de las distancias a todos los demás nodos. La ecuación sería entonces:
Para ejemplificar este cambio, para el ejemplo de la red anterior, las distancias inversas y las puntuaciones de proximidad son:
| Nodes | Closeness | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | Sum | Normalized | ||
| A | … | 1.00 | 1.00 | 0.50 | 0.50 | 0.33 | 0.33 | 0 | 0 | 0 | 0 | 3.67 | 0.37 | |
| B | 1.00 | … | 1.00 | 0.50 | 1.00 | 0.50 | 0.33 | 0 | 0 | 0 | 0 | 4.33 | 0.43 | |
| C | 1.00 | 1.00 | … | 1.00 | 0.50 | 0.50 | 0.50 | 0 | 0 | 0 | 0 | 4.50 | 0.45 | |
| D | 0.50 | 0.50 | 1.00 | … | 0.50 | 1.00 | 1.00 | 0 | 0 | 0 | 0 | 4.50 | 0.45 | |
| E | 0.50 | 1.00 | 0.50 | 0.50 | … | 1.00 | 0.33 | 0 | 0 | 0 | 0 | 3.83 | 0.38 | |
| F | 0.33 | 0.50 | 0.50 | 1.00 | 1.00 | … | 0.50 | 0 | 0 | 0 | 0 | 3.83 | 0.38 | |
| G | 0.33 | 0.33 | 0.50 | 1.00 | 0.33 | 0.50 | … | 0 | 0 | 0 | 0 | 3.00 | 0.30 | |
| H | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 1.00 | 0.50 | 0 | 1.50 | 0.15 | |
| I | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.00 | … | 1.00 | 0 | 2 | 0.20 | |
| J | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.50 | 1.00 | … | 0 | 1.50 | 0.15 | |
| K | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | |
Esta medida se puede extender fácilmente a las redes ponderados mediante la introducción (1959) el algoritmo de Dijkstra tal como se propone en la distancia más corta media en redes ponderados.
Referencias
Dijkstra, E. W., 1959. A note on two problems in connexion with graphs. Numerische Mathematik 1, 269-271.
Freeman, L. C., 1978. Centrality in social networks: Conceptual clarification. Social Networks 1, 215-239.
Opsahl, T., Agneessens, F., Skvoretz, J. (2010). Node centrality in weighted networks: Generalizing degree and shortest paths. Social Networks 32, 245-251.
Wasserman, S., Faust, K., 1994. Social Network Analysis: Methods and Applications. Cambridge University Press, New York, NY.
Tore Opsahl
No hay comentarios:
Publicar un comentario